DFSS – 1. 중심적 경향과 산포도

어떤 표본 데이터가 있을 때, 그 데이터로부터 모집단에 관하여 추정할 수 있는 정보로는 모집단의 분포곡선, 그 분포의 중심위치, 산포도 등이 있다. 중심위치 경향의 측도 및 산포도의 측도에 대해서 정리해 본다.

중심위치 경향을 알 수 있는 여러 가지 측도

• 모집단의 평균과 산술평균 (Arithmetic Mean)

  가장 많이 사용되는 것이 산술평균 값이다. 평균을 계산하기 위해서는 데이터가 필요한데, 관심이 있는 모집단의 모든 데이터를 확보하는 것은 대부분의 경우 불가능하므로 모집단의 평균 (모평균, μ) 과 구별하기 위하여 표본평균이라 부른다. 대부분의 경우, 모평균 (μ)은 표본평균을 통해서 추정하게 된다.

  n개의 표본 데이터가 있을 때, 표본 평균은 다음과 같다.

  

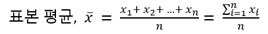
• 최빈값 (Mode)

  전체 데이터에서 가장 자주 나오는 값. 표본집단에 대한 대표치로 사용할 수 있다.

• 중앙값 (Median)

  표본집단이 n개의 데이터를 가질 때, n이 홀수라면 중앙에 위치하는 데이터이고, n이 짝수라면 중앙에 위치하는 두 개의 데이터의 평균치이다. 산술평균에 비하여 전체 데이터를 사용한다는 측면의 효율성에서 불리하다. 하지만, 데이터 중에 극단값 (outlier) 이 있다고 하고, 이 값이 표본평균의 사용에 영향을 줄 것을 우려한다면 중앙값 (Median) 을 사용하는 것을 검토해 볼 수 있다.

• 사분위수

  표본집단의 수, n이 매우 크다면 중앙값의 개념을 좀 더 확장하여, 데이터를 크기 순으로 4개의 집단으로 나누는 방법도 있다. 보통 최대값에서 최소값을 뺀 범위를 기준으로 0~25%, 25~50%, 50~75%, 75~100%로 나누고 그것을 다음과 같이 박스 그래프 (Box Plot)으로 나타낸다. 데이터의 대략적인 내용 (중심위치 경향, 대략적인 산포도, 극단값 유무 등) 을 알 수 있다.

  

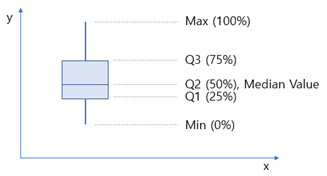
산포도의 경향을 알 수 있는 여러 가지 측도

데이터가 표본평균으로부터 어느 정도 퍼져 있는 가를 나타내는 측도이다. 다음과 같은 것들이 있다.

• 제곱합 (SS, Sum of Squares)

  제곱합이란 개개의 측정값과 표본평균 간의 편차의 제곱을 모든 데이터에 대하여 더한 것이다. 제곱을 하는 이유는, 그렇게 하지 않을 경우 음의 수와 양의 수가 서로 상쇄되므로 데이터가 퍼진 정도를 알 수 없기 때문이다.

  

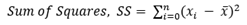
• 불편분산 (S², Unbiased Variance)

  제곱합 (SS)를 n-1 로 나는 것을 불편분산, S² 라고 한다. 표본크기 n에서 1을 뺀 n-1을 자유도 (degree of freedom) 이라고 부른다.

  

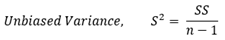
  모집단의 모든 데이터에 대해 불편분산 방식을 적용한 것을 분산, σ² 이라고 정의 하는데, 불편분산, S²는 모집단 분산, σ² 의 불편 추정량 (Unbiased Estimator) 이다. 모집단의 분산을 바로 구하기는 현실적으로 불가능한 경우가 많으므로 불편분산, S² 가 검정과 추정 과정에서 주로 사용된다.

  불편분산, S²는 상기와 같은 관계로, 간단히 분산 (Variance) 이라고 부른다. 하지만 모집단의 분산, σ² 와는 다른 의미임을 알아야 한다.

• 표준편차 (S, Standard Deviation)

  분산 (Variance)의 제곱근을 표준편차라고 한다.

  

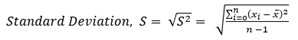
  표본 데이터가 어떠한 차원을 가진 물리량일 때, 분산을 계산 시 제곱을 하고, 표준편차 계산 시 다시 제곱근을 하게 되므로, 표본 데이터의 차원과 표준편차의 차원은 같다. 표준편차의 크기가 클수록 데이터의 경향이 산술평균으로부터 넓게 퍼져있는 것이다 (주어진 물리량을 기준으로).

  표준편차 S 를 단순히 σ 로 사용하기도 한다. 정확한 의미는 모집단 분산 σ² 의 제곱근이 σ 이다.

• 범위 (R, Range)

  표본 데이터 중에서 최대값과 최소값의 차이를 범위라고 한다.

  R = x_Max – x_Min

• 변동계수 (V_C, Coefficient of Variation)

  상기에 나열된 산포도 경향 측도 들은 어떠한 관심있는 물리량 (예들 들면, 거리 [mm] 단위) 에 대하여 단위를 [cm] 로 바꾸면 그 값이 변경된다. 따라서, 산포도 경향이 동일함에도 그 경향에 변동이 있었는 지, 아니면 단위 변경 때문인지 점검을 해 보아야 한다.

  만일, 두 가지 이상의 표본 집단이 있고, 그것을 비교해야 할 필요가 있을 때, 각 표본 집단에 정의된 단위가 서로 상이하다면 혼란이 생기게 된다. 이런 경우에 변동계수 (V_C)를 사용하면 혼란을 피할 수 있다.

  

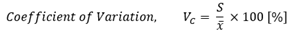
  표준편차, S와 표본평균의 단위가 같고, 분자/분모에서 서로 상쇄 되므로, 변동계수 V_C는 단위 변경에 영향을 받지 않는다.