이산확률분포(Discrete Probability Distribution)는 수를 세는 경우에 나타나는 결과 값의 분포를 의미한다. 값이 연속되지 않는 특징이 있으며, 표본의 개수가 셀 수 있을 만큼 존재한다고 생각할 수 있다. 이산확률분포의 형태는 다음의 4가지가 있다.
- 베르누이분포 (Bernoulli Distribution)
- 이항분포 (Binomial Distribution)
- 초기하분포 (Hypergeometric Distribution)
- 포아송분포 (Poisson Distribution)
연속확률분포(Continuous Probability Distribution)는 데이터 수집장치 등으로부터, 무게, 시간, 압력, 길이 등의 값을 측정하는 경우와 같이, 값이 서로 연속적이며 크기가 표본의 개수가 상대적으로 크다. 확률변수 X값을 어떠한 것으로 특정하기가 힘든 특성이 있다. 아날로그 신호와 그것을 샘플링 할 때의 이산(Discrete)와 혼동해서는 안 되며, 이 경우의 샘플링 된 이산 값 (discrete data with constant sampling period)는 연속확률분포(Continuous Probability Distribution)로 해석되어야 한다. 연속확률분포의 형태는 다음의 4가지가 대표적이다.
- 정규분포 (Normal Distribution)
- t 분포 (t-Distribution)
- F 분포 (F-Distribution)
- 지수분포 (Exponential Distribution)
이산확률분포 → 베르누이분포 (Bernoulli Distribution)
이산확률분포에서 가장 기초적인 것이다. 동전을 던져서 앞면이 나오면 성공, 뒷면이 나오면 실패라고 가정해 본다. 각각의 확률은 1/2이다. 이렇게 단순히 어떤 시행의 결과가 성공 때는 실패 두 가지만 있는 시행 (trial)을 베르누이 시행(Bernoulli Trial) 이라고 한다. 여기서 확률변수 X를 시행이 성공을 때 1을 갖고, 실패일 때 0을 갖도록 정의하면, 이 확률변수 X를 베르누이 확률변수 (Bernoulli Random Variable) 이라고 한다.
동전 시험의 경우와 같이 확률이 반드시 1/2일 필요는 없다. 가능한 결과가 오직 2개인 경우이어야 베르누이 시행이 된다. 시행, 성공과 실패 확률, 확률 변수 등을 다음과 같이 각각 정의하면,
- 시행의 결과: 성공(S), 또는 실패(F)
- 성공 확률: p = P(S)
- 실패 확률: q = P(F) = 1 – p
- 확률 변수: X = 1 은 성공을 의미, X = 0은 실패를 의미함.
이때 확률변수 X의 확률밀도함수 (PDF, Probability Density Function)는 다음과 같다.
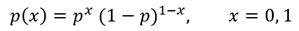
이것을 베르누이 분포의 확률밀도 함수(PDF of Bernoulli Distribution) 라고 한다.
확률변수 X의 기대값 E(X)과 분산 V(X)은 다음과 같다.
-
E(X) = p
= 1* p + 0 * (1 – p)
-
V(X) = p (1 – p)
E(X^2) = 1^2 * p + 0^2 * (1 – p) = p
V(X) = E(X^2) – E(X)^2 = p – p^2 = p(1 – p)
이산확률분포 → 이항분포 (Binomial Distribution)
성공률이 p인 베르누이 시행이 n번 반복 시행되었을 때, 확률변수 X를 “n번 시행에서의 성공횟수”라고 정의하자. 이때 X의 확률분포를 시행횟수 n과 성공률 p를 갖는 이항분포 (Binomial Distribution) 이라고 한다. 이항분포를 B(n, p)라고 정의하고, n은 시행횟수를 의미하므로 X가 취할 수 있는 값은 0, 1, 2, … , n 이 된다.
이항분포 B(n, p)의 확률밀도 함수(PDF of Binomial Distribution)는 다음과 같다.
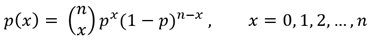
여기서 앞 부분에 있는 이항계수, 2×1 행렬은 조합 nCX = n! / ( x! (n-x)! ) 를 의미한다.
이항분포가 품질관리에 사용되는 예는 다음과 같다. 불량률이 p 인 관리상태에 있는 어떠한 공정이 있다고 하자 (이를 무한 모집단으로 생각할 수 있다). 여기에서 크기가 n인 표본을 취하는 경우가 있을 수 있다. 또는 불량률이 p 인 어느 한 제품의 Lot (보통 1 batch에서 생산되는 량) 이 있다고 한다 (이를 유한 모집단으로 생각할 수 있다). 여기에서 크기가 n인 표본을 복원 추출 (sampling with replacement; 샘플 한 개를 취하고, 측정을 한 다음 그것을 유한 모집단에 되돌려 넣고, 이 과정을 반복해 나가는 방법) 하는 경우가 있을 수 있다. 이 두 가지 경우에서, 표본 중에 발견되는 불량품의 개수 X는 이항 확률변수이다.
일반적으로 어떠한 속성 A (불량이라는 것도 하나의 속성에 해당한다)을 갖는 비율이 p 이고, 속성 A를 갖지 않는 비율이 q = 1 – p 인 무한모집단 또는 복원 추출되는 유한모집단에서 크기 n의 표본을 추출할 때, n개 중에서 속성 A를 갖는 개수 X는 이항분포 B(n, p) 에 따른다.
확률변수 X가 이항분포 B(n, p)를 따를 때, X의 기대값 E(X)과 분산 V(X)은 다음과 같다.
- E(X) = np
- V(X) = np(1 – p)
이항분포는 다음의 특징을 가진다.
- p = 0.5 일 때는 기대값 np에 대하여 이항분포 B(n, p)는 대칭이 된다.
- n p >= 5 이고, n (1 – p) >= 5 일 때는 이항분포 B(n, p)는 정규분포에 근사된다.
- p <= 0.1 이고, n >= 50 일 때는 이항분포 B(n, p)는 포아송분포에 근사된다.
이산확률분포 → 초기하분포 (Hypergeometric Distribution)
초기하분포는 불량률 p를 어느 한 제품의 Lot (보통 1 batch에서 생산되는 량)에 대해 고려하는, 유한 모집단의 경우와 같은 분석에 사용된다 (무한 모집단은 고려하지 않음). 이때 한 Lot의 크기는 N으로 정의하고, 추출하는 표본의 크기는 n으로 정의한다.
이항분포와 초기하 분포의 차이점은 이항분포가 유한 모집단일 경우 복원추출을 해야 하는 것에 반해, 초기하 분포는 유한 모집단에서 비복원추출을 한다는 점이다.
초기하분포의 확률밀도 함수(PDF of Hypergeometric Distribution)는 다음과 같다.
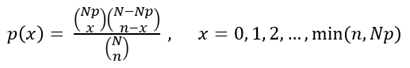
확률변수 X가 초기하분포를 따를 때, X의 기대값 및 분산은 다음을 따른다.
- E(X) = np
- V(X) = ((N – n) / (N – 1)) npq, q = 1 – p
또한 표본의 불량률 p’ = X/n 는 다음과 같은 기대값과 분산을 가진다.
- E(p’) = p
- V(p’) = ((N – n) / (N – 1)) (pq/n), q = 1 – p
이산확률분포 → 포아송분포 (Poisson Distribution)
어떤 확률변수 X가 x = 0, 1, 2, 3, … 을 취할 수 있고 그것의 확률밀도함수(PDF, Probability Density Function)가 다음을 따른다면, 포아송분포라고 부른다.
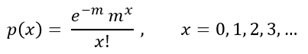
단위 시간 내에 걸려오는 전화 수, 어느 고속도로에서 하루에 발생되는 교통사고의 수 등은 포아송분포로 잘 설명된다고 알려져 있다.
확률변수 X가 포아송분포를 따를 때, X의 기대값 및 분산은 다음을 따른다.
- E(X) = m
- V(X) = m
포아송분포는 다음과 같은 특징을 가진다.
- 기대값과 분산이 같다.
- m >= 5 이면, 포아송분포는 정규분포에 근사된다.
- M 이 작을 때는 오른쪽으로 긴 꼬리를 가진 분포가 되나, m 이 커짐에 따라 대칭에 가까워 진다.
연속확률분포 → 정규분포 (Normal Distribution)
정규분포는 대표적으로 널리 사용되는 연속확률분포이며, 가우스분포 (Gaussian Distribution) 이라고도 한다. 정규분포는 자연과학 및 사회과학에서 어떤 변수가 무작위로 가질 수 있는 실제 값에 관한 분포를 기술하는 데 유용하게 사용된다. 그 원리는 중심극한정리(Central Limit Theorem)에 기인한다. 이는 확률분포에 대해 미리 알려지지 않은 어떠한 변수가, 정해진 횟수 n 만큼 복원 추출하는 작업을 반복했을 때, 그 추출된 값들의 평균값은 n이 커짐에 따라 정규분포에 접근한다는 정리이다.
확률변수 X의 기대값이 μ이고, 표준편차가 σ일 때, 그 확률밀도함수 (PDF, Probability Density Function)가 다음의 식을 따르면, 확률변수 X는 정규분포 N(μ, σ2)를 따른다 고 한다.
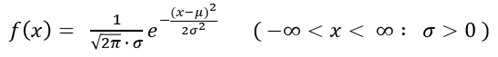
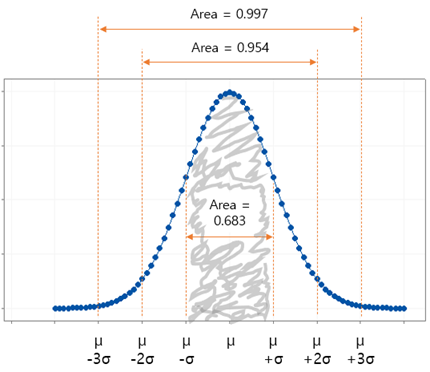
확률밀도함수의 정의에 따라, 그 함수의 면적은 항상 1이 되며 (100%), 특정 확률변수 구간에 의해 정해지는 면적은 해당 구간에서의 확률이 된다. 정규분포에서는 기대값 μ와 표준편차 σ에 의해 다음과 같이 그 면적이 결정된다. “면적 = 확률” 이므로, 아래 수식에서 P[ … ] 로 표기하였다. 향후, 공정관리도 및 관리 능력에 대한 지표에서 중요하게 사용되는 값이다.
- P [ μ
– σ < X < μ
+ σ ] = 0.683 (= 68.3 %) - P [ μ
– 2σ < X < μ
+ 2σ ] = 0.954 (= 95.4 %) - P [ μ
– 3σ < X < μ
+ 3σ ] = 0.997 (= 99.7 %)
이 확률밀도함수를 확률변수 X를 수평축으로 하여 그래프로 나타내면 다음과 같다. 기대값 μ를 기준으로
정확히 좌우대칭이다. 확률변수X의 값이 좌,우 방향으로 무한대로 가면 면적은 1에 근사한다.
확률밀도함수를 다음과 같은 조건에 의해 변수변환을 하게 되면, 표준정규분포(Standard Normal Distribution)가 된다.
- 기대값 μ = 0
- 표준편차 σ = 1
- 변수변환, Z = (X – μ) / σ
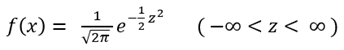
이 수식에 따른, 표준정규분포 확률밀도함수 그래프는 다음과 같다.
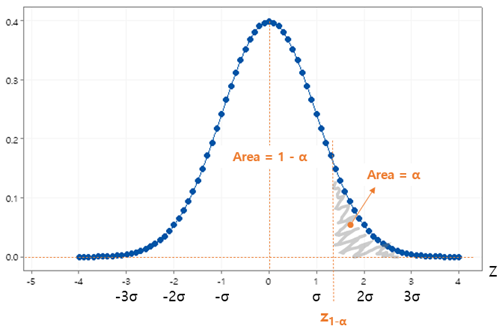
이 그래프에서는 누적확률 (Cumulative Probability)인 (1 – α) 도 표기하고 있다. 이 누적확률 (1 – α)를 수식으로 나타내면 다음과 같다.
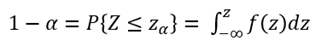
확률밀도함수의 적분 결과인, 누적확률 그래프는 다음과 같다.
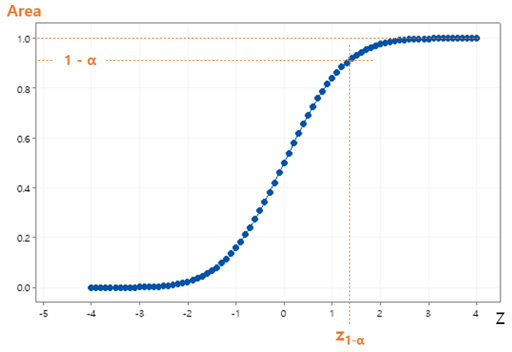
표준정규분포와 표준누적확률은 미리 계산되어진 표가 있으며, 이를 참고하면 편리하게 정규분포를 이용한 확률통계분석을 수행할 수 있다.
연속확률분포 → t 분포 (t-Distribution)
두 확률변수 Z 와 χ2 이 서로 독립적이며, Z는 표준정규분포 N(0, 1)에 따르고, χ2은 자유도 ψ 인 카이제곱분포 χ2 를 따를 때, 확률변수 T를 다음과 같이 정의한다. 이 확률변수 T는 자유도 ψ인 t 분포를 한다.
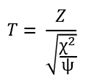
t 분포는 표준정규분포의 평균 (즉, 기대값 μ = 0) 인 0을 중심으로 좌우대칭이다. 정규분포와 비교하면 꼬리 부분이 두껍다. 하기에 t 분포 그래프의 예를 자유도 ψ가 각각 3, 15, 25일 경우로 비교해 보았다.
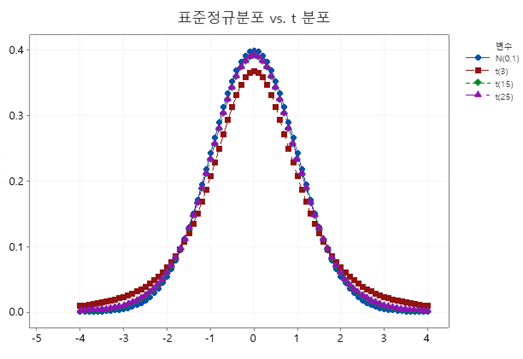
파란색 동그라미 표시가 표준정규분포 확률밀도 곡선 N(0, 1) 이다. 자유도 ψ가 3일 경우, t분포의 양측 꼬리 부분이 더 두꺼우나, 자유도가 증가해 가면 표준정규분포에 근사하는 것을 볼 수 있다.
연속확률분포 → F 분포 (F-Distribution)
두 확률변수가 다음과 같이 정의되고, 서로 독립이라고 하자.
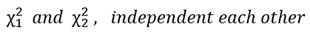
이 두 확률변수가 각각의 자유도 ψ1, ψ2를 가지고 카이제곱분포 χ2 를 따른다 고 하면, 다음 수식은 F 분포, F(ψ1, ψ2) 가 된다.
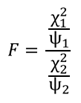
연속확률분포 → 지수분포 (Exponential Distribution)
지수분포 (Exponential Distribution)은 신뢰성 공학에서 많이 취급된다.
어떠한 제품은 제품출하검사에서는 정상 통과했으나 동작기간이 경과함에 따라 고장을 일으킬 수 있다. 이 고장률을 λ(t)라고 정의하자. 이 변수는 제품의 평균 동작 시간 (사용중인 제품의 전체 개수 x 각 제품의 평균동작시간) 동안 몇 개의 제품에 고장이 발생하는 지를 확률로 표기한 것으로 정의된다. 동작 시간에 따른 이 λ(t)는 다음과 같은 욕조곡선(bath-tub failure rate curve)을 따른다.
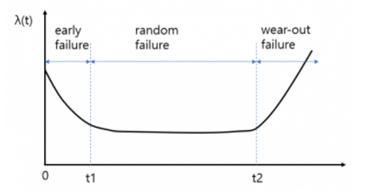
욕조곡선은 다음의 세 가지 단계, 초기고장 (Early Failure), 우발고장 (Random Failure), 마모고장 (Wear-out Failure)를 가진다.
-
초기고장 (Early Failure), 동작 기간 0 ~ t1 :
주로 제품에 내제하고 있는 설계나 제조 공정상의 결함에 기인하며, 그 결함을 찾아내어 안정화 할 필요가 있는 기간이다. 잘 설계된 제품이 적절한 품질계획에 따라 제조되었다면 회피할 수 있는 가능성이 높아지는 것이므로, 이러한 초기고장은 시스템적 고장 (Systematic Failure) 분류에 속한다.
-
우발고장 (Random Failure), 동작 기간 t1 ~ t2 :
동작시간이 일정 기간을 지나가면 (> t1), 제품의 고장률은 통계적으로 낮아지고, 시스템적인 고장 보다는 다른 원인으로 고장이 발생한다. 이는 제품을 구성하는 부품 및 재료 등이, 제품수명주기 이내에서 고장을 일으키는 것이며, 그 원인은 과중한 동작부하, 과중한 동작온도조건, 사용자의 조작 과오 또는 적절하지 않은 사용방법, 낮게 설정된 설계안전계수 등이 있을 수 있다. 이를 회피하기 위해서는 신뢰성이 높은 부품 또는 재료 사용, 극한 상황 및 높은 안전계수 설정 등을 통한 강건설계 등을 해야 한다. t1 ~ t2 기간 동안에 우발적으로 발생하는 이러한 고장을 우발 고장 (Random Failure)라고 한다.
-
마모고장 (Wear-out Failure), 동작 기간 t2 ~ :
이 기간은 제품이 동작 수명에 도달하여, 그 제품을 구성하는 재료나 하위부품의 기대 수명에 따라, 고장률이 급격하게 증가하기 시작하는 단계를 말한다. 이 단계에서는 제품을 폐기 또는 교체 (예방정비를 한다면, 좀 더 일찍) 해야 한다.
어떠한 제품 또는 부품의 고장률을 결정하는 방법은 여러 표준기관에서 다양하게 제시하고 있으나, 그 기본은 지수분포를 따르는 것이다. 여기서는 매우 기초적인 부분만 정리하도록 한다.
지수분포를 기본으로 표기하는 이러한 고장률이 다루는 동작기간은 초기고장기간(0 ~ t1) 및 우발고장기간(t1 ~ t2)이다. 상기 욕조곡선에서 이 기간 동안의 그래프가 지수함수곡선 모양임을 알 수 있다.
만일, 고장률 λ(t)가 시간에 관계없이 일정한 상수라고 하면 ( λ(t) = λ ), 고장 발생시간으로 정의되는 확률변수에 대하여 그 확률밀도함수는 다음과 같이 표현할 수 있다.
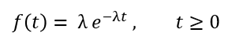
확률변수는 상기 수식에서, 시간 t 가 된다. 지수 분포를 하는 확률변수 T에 대한 기대값과 분산은 다음과 같다.
- E(T) = 1 / λ
- V(T) = 1 / λ2
여기서 고장까지의 평균시간 (MTTF, Mean Time To Failure) 및 평균고장간격 (MTBF, Mean Time Between Failures) 의 개념을 생각해 볼 수 있는데, 이 두가지 모두 상기 기대값 E(T)와 같다고 가정할 수 있다. 즉 MTTF = MTBF = 1 / λ 가 되며, 평균수명을 고려하는 가 (MTTF), 또는 제품의 교체주기를 고려하는 가 (MTBF) 에 따라 다르게 사용되는 것이다. 실제 산업계에서 사용되는 표준은 이보다 매우 복잡하며 사용되는 부품의 종류, 환경조건에 따라 달라진다. 자동차 산업분야의 경우에는 SN29500 또는 ICE TR 62380 규격집을 참고하면 된다.
상기 확률밀도함수의 그래프는 하기 예시와 같을 수 있다.
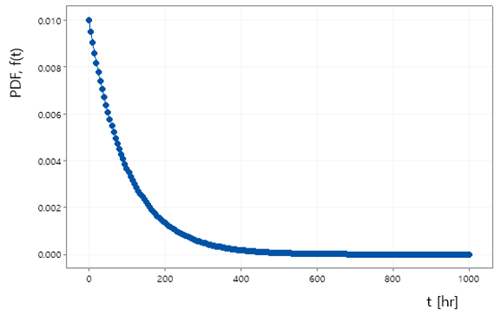
제품의 동작 시간을 0 ~ 1000 [hr] 까지, 고장률 λ = 100으로 둔 경우의 그래프이다. 확률밀도함수를 적분하여 누적확률을 구하면, 다음 수식과 같다.
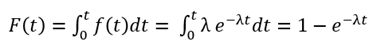
지수분포는 주로 고장률 계산에 사용되므로, 이 적분 결과를 누적고장곡선 (Cumulative Failure Curve)라고도 부른다. 상기 확률밀도함수의 조건으로 누적고장곡선을 나타내면 다음과 같다. 이 그래프의 수직 축은 어떤 t 시간 후, 고장이 나 있을 확률이 된다.
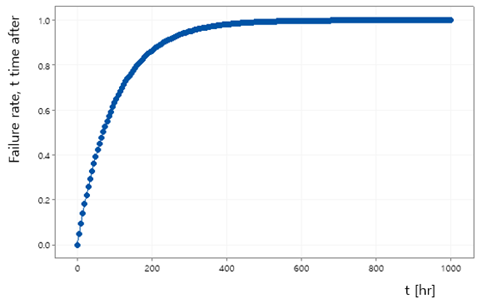
실제의 경우에는 도저히 출하할 수 없는 매우 높은 고장률로, 상기 그래프가 지수함수 형태를 나타낸다는 것을 보여주기 위해서 과장한 수치이다. 자동차 산업계에서는 FIT (Failure In Time)이라는 것을 사용하는데, 실제 제품의 고장률은 매우 낮게 유지되어야 하므로 보통 109 시간 동안 몇 개가 고장이 나는 가를 척도로 한 것이다.