기능안전 (Functional Safety)에서 Failure Rate 항목에 대해 정의할 때 Reference Temperature 나 신뢰수준(Confidence Level)이라는 용어를 자주 접하게 된다. 이는 원래 통계학에서 쓰이는 것이고 DFSS (Design for Six Sigma) 과정에서도 중요하게 사용된다. 이번 Posting에서는 이 주제와 관련되어 있는 모집단 특성의 추정 (모수의 추정) 및 신뢰수준 (Confidence Level) 에 대하여 정리해 본다.
모수의 추정 (Estimation of Population Parameter)
어떠한 모집단의 특성을 수량적으로 표시하는 방법으로는 기대치(평균), 분산, 표준편차 등이 사용된다. 이 항목들은 어떠한 데이터의 집합의 특성을 나타내는 상수 값이며, 그것이 어떠한 모집단 자체에 대한 특성을 나타낸다면 모평균, 모분산, 모표준편차 등이 된다. 이 값을 통틀어 모수(population parameter) 라고 한다. 이 값들을 구하기 위해 모집단 전체 시료를 모두 조사하는 것은 대부분의 경우 불가능하기 때문에 표본 시료 집단을 조사하게 된다. 이 표본 시료에 대한 평균, 분산, 표준편차를 모수(population parameter)에 대비되는 개념으로 통계량(statistics)라고 정의한다.
어떠한 표본들의 집합이 여러 개 있다고 하고, 모두 같은 모집단에서 나왔다고 해도, 각 표본들의 통계량은 서로 다를 확률이 더 높다. 따라서 어느 표본의 통계량이 모집단의 특성을 더 정확하게 정의하는 지 알기 힘들다. 여기서 통계량인 평균, 분산, 표준편차는 각 표본집단마다 다른 값을 가질 수 있는 확률변수이다. 통계량에 포함되는 항목은 이외에도 비율, 범위, 중앙값 등이 있을 수 있다.
모수와 통계량의 확률변수는 확실히 구분하여야 한다. 대표적으로 사용되는 기호 및 그 정의는 다음과 같다. 모수의 추정값과 통계량은 엄밀히 말하자면 같은 값은 아니다 (추정값 = 추정된 통계량의 의미). 이것을 대/소문자로 구분하기도 한다 (표에서 보이는 예와 같음).
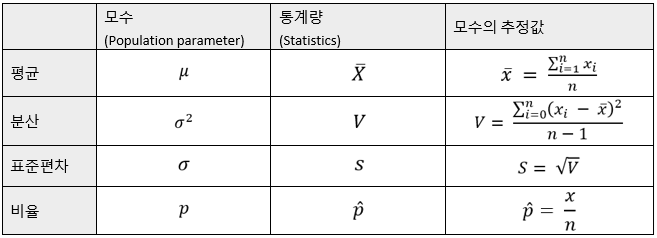
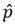는, 예를 들어, 그 값이 어떠한 표본 집단의 표본크기가 n 이고, 그 중에서 불량품의 개수가 x라면, n개의 제품 중 불량품 x개의 비율이다.
표본의 통계량으로부터 모수를 추정하려면 통계량 자체의 분포를 알아야 한다. 이를 위해서 모집단으로부터 같은 샘플 사이즈 (sample size, 표본크기), n을 가지는 표본집합을 k 개 하였다고 하자. 다음의 표와 같이, 각 표본집합의 통계량은 첨자를 이용해서 구분할 수 있다.
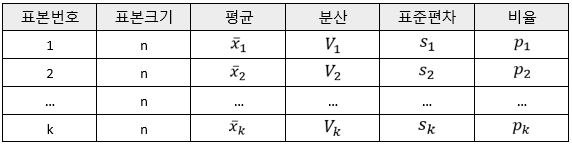
상기 표에서, 모집단이 정규분포 N(μ, σ2) 인 경우만 생각해본다. 또한 모집단은 무한모집단이고 (예를 들면, 양산라인에서 제조되는 부품), 표본의 추출(Sampling)은 랜덤하다고(Random Sampling) 가정한다. 그러면 k개의 표본집합들로부터 모수를 추정한다는 것은 무슨 의미일까?
어떤 모집단의 확률변수 x에 대한 확률밀도함수(p.d.f)가 f(x; θ)라고 하자. 여기서 θ는 미지의 모수로, 이 값을 모집단으로부터 얻어진 표본집합으로부터 추측해야 한다고 하자. 예를 들어, 어떤 공정에서 생산되는 제품의 무게가 정규분포 N(θ, (5)2) 을 따른다면, 정규분포 식에 의해 그 확률밀도함수(p.d.f)는 다음과 같다.
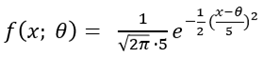
여기서, θ는 제품의 평균 무게를 나타내는 모수로, 위의 표에서 μ에 해당하는 것이다.
표본집합은 1개 이상인 k 값을 가질 수도 있고 k=1 (표본을 한 번 만 추출함) 일 수도 있다. K = 1인 경우, 일반적인 평균, 분산, 표준편차, 비율의 식 등을 사용할 수 있고, 만일 k가 1보다 크다면 각 표본집합에서 나온 표본 통계량 (평균, 분산, 표준편차, 비율)을 어떠한 규칙에 의해 구하여 모수의 추정에 사용할 수도 있을 것이다.
예를 들어 모집단으로부터 표본크기 n인 k개의 표본집합을 만들었다고 하자. 이 표본집합들의 통계량으로부터 어떠한 함수 φ (x1, x2, x3, …, xk)를 이용하여 모수를 추정할 수 있을 것이다. 간단한 예로, 모평균의 추정을 한다고 하면, 함수 φ는 다음과 같을 수 있다.
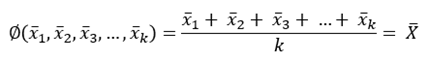
다른 표본 통계량 (분산, 표준편차, 비율 등)에 대해서도, 해당 표본 통계량 계산에 대한 공식이 이미 적용이 되었으므로, 직관적으로, 이들 값의 평균으로부터 모수를 추정할 수도 있을 것이다.
그렇다면, 이렇게 얻어진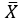 
는 모집단의 평균을 나타내는 모수인가? 그렇지 않고, 모수를 추측하는 추정량이다. 그렇다면 이 결과는 어떻게 신뢰할 수 있는가? 여기서 신뢰수준 (Confidence Level)에 대한 지표가 나온다.
신뢰수준 (Confidence Level)
모수의 평균을 나타내는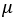 
에 대하여 점추정량(point estimator)을 정의하고 그것을 기호에 hat(^)을 붙여서 
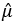라고 하자. 점추정량은 말 그대로 모수의 참값을 하나의 (점) 추정량으로 나타내는 것이다. 모수의 참값과 점추정량이 정확히 일치하는 경우는 거의 없을 것이다.
모수를 추정하는 다른 방법으로는 점추정량 대신에, 모수가 포함되리라고 예상되는 구간을 제시하는 것이다. 이와 같이 어떤 구간이 모수를 포함하고 있을 것이라고 추정하는 것을 구간추정 (Interval Estimation)이라고 한다. 그렇다면 어떠한 신뢰구간 (Confidence interval) 이 모수를 포함하고 있을 확률이 얼마나 되는 지를 알아야 할 것이다. 이것을 신뢰수준 (Confidence Level)이라고 부른다. 이것은 구간 값이므로 상한/하한이 존재할 것이다. 이 상한/하한 값을 신뢰한계 (Confidence Limit) 이라고 정의한다.
신뢰한계는 통계량이므로 표본에 따라서 달라지며, 그 폭은 신뢰수준에 의해 결정된다. 만일 신뢰수준이 95%라면, 그 신뢰구간이 모수를 가질 확률이 0.95라는 뜻이다.
모평균의 추정
모평균이 μ, 분산이 σ2 인 모집단에서, k=1이라고 하고 (즉, 간단한 예로, 표본집단을 한 번만 추출), 확률분포 x1, x2, x3, … , xn을 추출하여 표본평균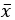 
를 구하면, 이는 다음과 같은 성질을 갖는다.
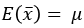이므로, 
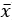는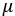 
를 중심으로 분포되어 있다.-
표본의 평균인
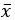도 모수의 통계량이므로 표준편차를 가진다. 이 표준편차를 
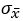라고 정의하면, 다음과 같이 모수의 표준편차 
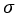로 계산할 수 있다.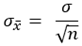
-
만약 모집단이 정규분포를 한다면
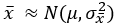이며, 다음의 관계가 있다.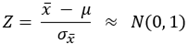
- 만약 모집단이 정규분포가 아니더라도
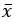는 n이 증가함에 따라 
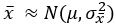에 접근한다. 이는 중심극한의 정리에 기초를 두고 있다.
여기서 한 가지 문제가 있는데, 상기 식에는 모수의 표준편차 σ를 알고 있어야 한다. 대부분의 경우 모수의 표준편차는 알려지지 않았을 수 있다. 따라서, 다음과 같이 모수의 표준편차를 알고 있는 경우와 알지 못하고 있는 경우로 나누어서 모평균을 추정하는 과정에 대해 정리한다.
모수의 표준편차, σ를 알고 있는 경우
모집단이 정규분포를 하면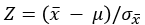 
는 표준정규분포를 따른다. 표준정규분포표에서, 확률변수 Z가 -1.96 ~ 1.96 사이에 있을 확률은 0.95이다. 따라서, 다음과 같이 수식을 전개할 수 있다.
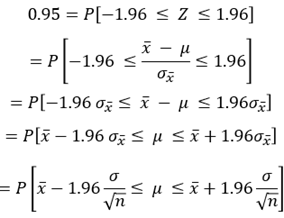
결론적으로 신뢰도 (Confidence Level) 95%를 가지는 신뢰구간 (Confidence Interval)은 다음과 같다.
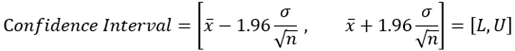
이 결과를 일반적인 공식으로 정의하면, 모집단이 정규분포를 따르고 표준편차 σ를 알고 있는 경우, 1 – α 의 신뢰도를 갖는 모평균 μ의 신뢰구간은 다음과 같다.
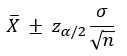
통계 소프트웨어 Minitab 에서는 “통계분석 / 기초통계학 / 1-표본 Z검증”에서, 이 값을 추정할 수 있다 (모수의 표준편차 σ가 알려진 경우).
모수의 표준편차, σ를 모르는 경우
이 경우에는, 상기에서 유도된 식을 사용할 수 없다. 모집단이 정규분포를 하고 있으나 σ를 모르는 경우에는 다음의 식으로 모집단의 평균 μ를 구한다. 표본집단의 분산 (V = s2) 을 이용하여 확률변수 T는, 자유도가 (n-1)인 t 분포를 따른다.
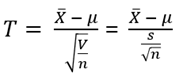
따라서 신뢰도가 1 – α 인 모평균 μ 의 신뢰구간은, t 분포곡선을 이용하여, 다음과 같이 정의된다.
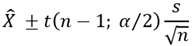
하지만, n이 충분히 커진다면, t 분포는 표준정규분포에 수렴하므로 (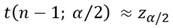
), 다음과 같은 수식을 사용할 수 있다 (좀 더 간단). 결국에는, n이 충분히 큰 경우라면, 모수의 표준편차를 표본집합의 표준편차로 사용하는 것이다.
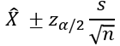
통계 소프트웨어 Minitab 에서는 “통계분석 / 기초통계학 / 1-표본 t검증”에서, 이 값을 추정할 수 있다 (모수의 표준편차 σ를 모르는 경우).
신뢰도 (Confidence Level) 및 신뢰구간 (Confidence Interval) 을 먼저 정의하고, 이를 만족하기 위한 샘플의 개수를 알고자 하는 경우
모평균을 구간 추정할 때에는 신뢰구간의 폭이 좁은 것이 좋으며, 표본의 크기 n이 증가함에 따라 이 값은 작아진다. 따라서 n의 값이 커지는 것이 좋다. 하지만, 이 값이 커질수록 경비와 시간이 많이 소요되므로 제한 요소가 된다. 따라서 주어진 정밀도 (신뢰도 및 신뢰구간) 을 만족하기 위한 표본의 크기를 사전에 결정하는 것이 필요할 것이다.
모집단이 정규분포를 따른다고 가정하고, 모평균 μ의 추정에서 100 (1 – α) % 오차한계는, 앞서 살펴본 바와 같이 다음과 같다.
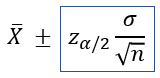
이 수식의 의미에 따라, 오차가 지정된 값 d 를 초과하지 않는다고 100 (1 – α) % 확신하기 위해서는 표본크기 n은, 이 수식을 만족해야 할 것이다.
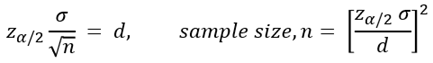
예를 들면, 공장에서 생산하는 어떠한 제품의 무게가, 오랜 세월 동안 축적한 자료에 의하여 표준편차가 50 gram 이라고 하면, 90% 의 신뢰도를 갖고 신뢰한계 추정오차가 3 gram 를 가지도록 할려면, 얼마나 많은 표본의 크기를 가져야 하는가?
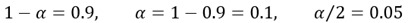
이고, 표준정규분포에서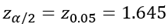 
이므로,
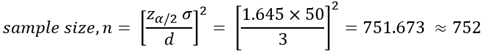
이 결과에 따라, 752개의 샘플을 추출하여야 한다.