어떤 공정에서 나오는 제품의 품질특성은 해당 규격에 완전히 일치하도록 지속적으로 생산을 하는 것이 가장 이상적이다. 하지만, 흔히 4M으로 불리는 Man, Machine, Material, Method에 의한 변동요인과, 환경적인 요인 들로 인해 영향을 받으므로, 이 목표를 달성하는 것은 불가능하다. 따라서 통계적인 방법으로 어떠한 공정의 공정능력지수 Cp, Cpk 또는 공정성능지수 Pp, Ppk를 정의하게 된다.
다음의 표와 같이 Cp / Cpk / Pp / Ppk 의 정의를 구분해 두었다.

공정능력지수 Cp의 계산에서 표준편차 σ는 군내변동 (within group variation)을 나타낸다. USL, LSL은 어떠한 규격의 상한 (Upper Standard Limit) 및 하한 (Lower Standard Limit)을 의미한다. 만약 규격의 중간값 (M = (USL+LSL)/2) 이 기대값과 일치하지 않으면 (대부분의 경우에 해당한다), 치우침의 영향도를 고려해야 한다 (변수 K 값). Cpk가 이 경우에 해당하며, Cpk는 이 수식의 정의에 따라 Cp보다 작거나 같다. 따라서 Cpk는 공정능력지수를 정의하는 데 있어서 좀 더 엄격하게 사용된다 (Cp, Cpk가 클수록 공정능력이 좀 더 좋음을 의미).
공정성능지수 Pp및 치우침을 고려한 Ppk는 Cp, Cpk와 유사한 수식을 사용한다. 하지만, 표준편차를 구하는 방식이 틀린데, Cp의 계산에서는 군내변동 (within group variation) 만 고려했다면, Pp계산에서는 군간변동 (between group variation)까지 고려한다. 군간 변동이 없는 이상적인 경우라면 Cp와 Pp는 같다. 하지만, 이러한 경우는 매우 드물며, Pp는 Cp보다 작은 값을 가진다. 따라서 공정성능지수 Pp는 공정능력지수 Cp에 비해 좀 더 엄격하게 적용되는 값이다.
좀 더 자세히 알아보자.
공정능력지수, Cp and Cpk
양쪽 규격 (USL, LSL) 이 정의되는 경우, Cp에 대한 수식은 앞서 살펴본 바와 같다. 즉, 공정능력지수의 의미는 규격의 상한/하한 폭을 표준편차와 비교한 것이다.
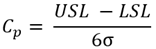
이 정의에 따라, Cp = 1 이 되는 조건을 정규분포도로 그려보면 다음과 같다.
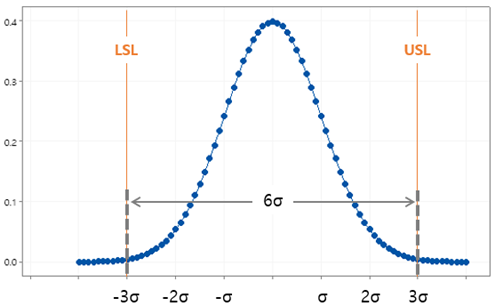
USL, LSL이 이 경계보다 넓어지면 Cp > 1 가 되고, 좁아지면 Cp < 1이 된다. 정규분포도에서 6σ (+/-3σ)범위가 차지하는 면적은 0.997 (99.7%)이므로, USL/LSL을 그림과 같이 설정한 경우 규격을 벗어나는 제품의 불량율은 0.3% (소수점을 좀 더 고려하면, 0.27%)가 될 것이다.
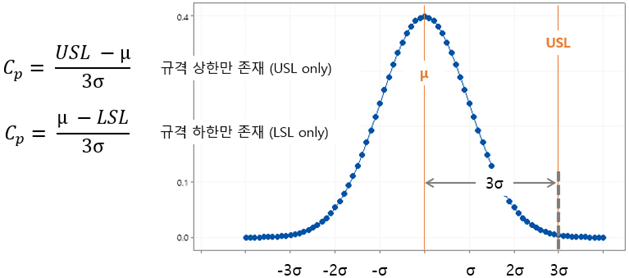
만일, 한쪽 규격만 있는 경우라면, 수식 및 정규분포도는 다음과 같다. μ는 모집단의 평균이다. 실무적인 상황에서는 한 쪽 규격만 있는 경우가 더 많을 수 있다.
공정능력지수, Cp and Cpk
Cp에서는 공정의 평균이 규격의 중간 값을 벗어나면 바로 불량률에 영향을 주게 된다. 이것이 좀 더 일반적인 상황이므로, Cp보다는 공정능력에 치우침이 있는 경우를 나타내는 Cpk 지수를 많이 사용하게 된다.
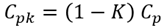
여기서, 치우침도 K는 다음의 그림에서 와 같이 정의된다.
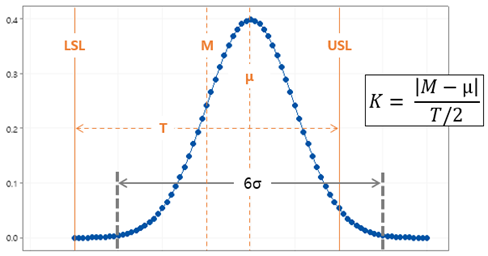
- M은 규격의 중간 값을 의미. M = (USL + LSL) / 2
- T는 규격의 폭을 의미. T = USL – LSL
- 만일, K = 0 이라면, Cp = Cpk 인 이상적인 경우가 된다.
- K >= 1 이 되면, 치우침이 매우 큰 상태를 의미하며 Cpk는 음의 값을 가진다. 이는 공정능력이 대단히 불량함을 의미하며, 보통은 발생하지 않는다.
- 상기 Cpk 및 K값 관련 수식은 양쪽 규격, 한쪽 규격 모두에 동일하게 적용된다.
공정능력지수와 시그마 수준의 관계
보통 공정능력이 3시그마, 4시그마 수준이라는 표현을 많이 사용할 것이다. 이것의 정확한 의미는, σ 의미를 한쪽 규격일 경우를 이용하여 μ와 USL (또는 LSL) 사이에 몇 개의 σ가 들어가는 지를 말하는 것이다. 아래 그림과 같이 3개의 σ가 들어가도록 USL을 설정하면, 수식에 따라 Cp = 1 이 되고 (양쪽 규격에서 σ가 USL – LSL 사이에 6개가 들어가는 것과 동일함), 공정능력에 따라 Cp는 변동이 된다. Cp가 클수록 공정능력이 좋은 것이다.
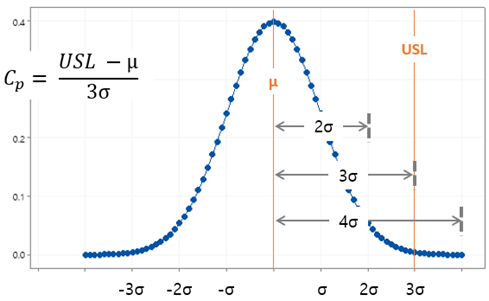
시그마 수준과 Cp의 관계를 다음의 표와 같이 정리해 두었다.

공정능력을 평가하는 기준은 해당 조직마다 다르겠지만, 일반적으로 다음의 기준으로 생각할 수 있다.
- Cp >= 1.67 5 Sigma 수준. 공정상태가 매우 우수. 공정 산포도 관리도 매우 우수.
- 1.33 <= Cp < 1.67 4 Sigma 수준. 공정상태가 양호. 공정산포도 관리도 만족스러움.
- 1.00 <= Cp < 1.33 3 Sigma 수준. 공정상태를 받아들일 수는 있으나 시급한 개선이 필요함.
- 0.67 <= Cp < 1.00 2 Sigma 수준. 공정상태에 심각한 문제가 있으며, 부적합품이 다량 발생하고 있음.
공정성능지수, Pp and Ppk
앞서 살펴본 바와 같이 Pp는 군내변동 (within group variation) 및 군간변동 (between group variation)을 모두 고려한 것이다. 품질특성의 산포는 군내변동 뿐만 아니라, 군간변동에서도 올 수 있다. Pp로부터 Ppk의 정의는 Cp에서 Cpk를 정의한 것과 동일하다.
Cp (또는 Cpk) 와 Pp (또는 Ppk) 의 유일한 차이점은 표준편차를 구하는 방식에 있다. 다음 수식을 참고한다.
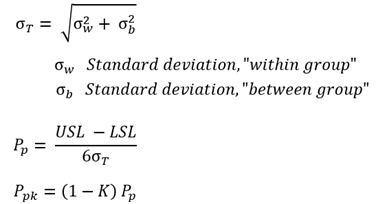
군내 변동 및 군간 변동을 모두 고려한 표준편차 σT는 각각의 경우보다 같거나 크므로, Cp >= Pp 또는 Cpk >= Ppk의 관계가 항상 성립한다.
Cp / Cpk는 제품의 개발과정에서 주로 사용된다. 군간변동을 측정하기에는 현실적인 어려움이 따르기 때문이다.
양산 제품에서는 Cp/Cpk와 Pp/Ppk가 서로 상보적으로 사용되는데, 예를 들면, 어떠한 생산라인이 단기간에 걸쳐 안정화 되어 있으나 (Cpk pass), 중장기간에 걸쳐 공정의 품질변동범위가 적절하게 유지되는 지를 알아보려면 Ppk를 측정해야 한다. 중장기간 품질에 영향을 줄 수 있는 요인들은 많이 있을 것이다. 원재료의 lot가 변경되었다던 지, 작업자의 rotation, 공구의 마모로 인한 신품 교체, 장비의 수리로 인해 전/후 간의 성능차이 발생 등이 있을 수 있다. Cpk와 Ppk의 값을 조사하여 이상원인을 규명하고 적절한 조치를 취해 주어야 한다.