기능안전의 HW part (ISO26262 – Part 5) 에서는 FIT (Failure In Time) Rate라는 정의가 중요하게 사용된다. FIT Rate의 정의 및 그와 유사하게 사용되는 MTTF (Mean Time to Failure), MTBF (Mean Time Between Failures) 에 대해 정리한다.
신뢰성 (reliability) 이란 용어는 어떠한 부품이나 시스템이, 그 제품 사양서에 기술된 대로 정상동작 할 수 있는 확률로 정의할 수 있다. 또한, 어떠한 제품이 무한한 수명을 가질 수는 없기 때문에, 어떠한 동작 조건에서 얼마나 오랫동안 정상동작 할 수 있는 지에 대한 확률적인 예측도 해야한다.
고장률 (λ, failure rate) 은 제품의 평균 동작 시간 (사용 중인 제품의 전체 개수 x 평균동작시간) 동안 몇 개의 고장이 발생했는 지를 확률로 표기한 것이라고 개략적으로 정의할 수 있는데, 다음과 같은 욕조 곡선 (bath-tub failure rate curve)를 따른다.
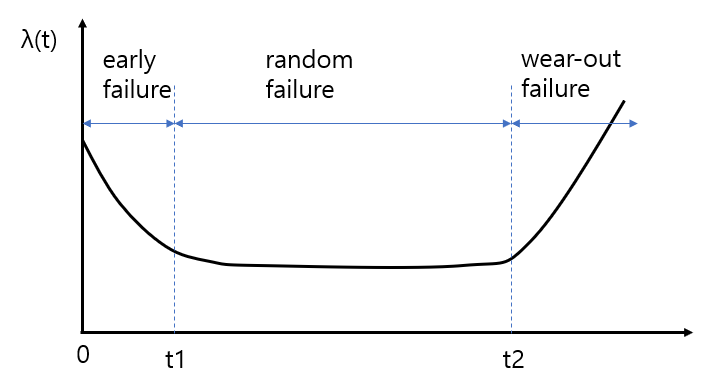
제품의 고장 형태는, 그림에서와 같이 세 가지 단계 (초기고장 early failure, 우발고장 random failure, 마모고장 wear-out failure) 를 가진다.
초기고장 (early failure)은 제품에 내재하고 있는 설계나 제조 공정 상의 결함에 기인한 것으로, 그 결함을 찾아내어 안정화 시킬 필요가 있는 시기이다. 잘 설계된 제품이 적절한 품질 계획에 따라 제조 되었다면 회피할 수 있는 가능성이 높아지는 것으로, 이러한 초기 고장은 시스템 적 고장 (systematic failure) 에 속한다.
일정 기간이 지나면 (> t1) 제품의 고장률은 통계적으로 낮아지고, 시스템적 고장 보다는 다른 원인으로 고장이 발생한다. 이는 제품을 구성하는 부품 및 재료 등이, 제품 수명 주기이내에서 고장을 일으키는 것이며, 그 원인은 과중한 동작 부하, 과중한 동작 온도 조건, 사용자의 조작 과오, 낮게 고려된 안전계수 등이 있을 수 있다. 그 대책으로는 신뢰성이 높은 부품이나 재료를 적용하거나, 극한 상황을 고려한 강건 설계, 더 높은 안전 계수 고려 등이 있을 수 있을 것이다. t1 ~ t2 기간동안, 이러한 이유로 발생하는 우발 고장을 random failure라고 한다.
기능안전의 HW part (ISO26262 -Part 5) 에서는 systematic failure 및 random failure를 구분하고 각각의 대책을 세우도록 요청하고 있다. 특히 random failure에 대한 분석 및 승객의 안전에 미치는 심각도를 조사하고, 그 제품 자체가 가지고 있는 안전 메커니즘 (safety mechanism)에 의해 random failure가 발생했을 때 해당 불량에 대해, 명시되어 있는 제한 시간내에 검출 및 적절한 조치를 취하도록 요구한다. 이 능력이 얼마나 되는 지가 (FMEDA, Failure Modes, Effects and Diagnostic Analysis) ASIL Level을 결정하는 중요 지표가 된다.
모든 제품은 수명이 있다. 이는 그 제품을 구성하는 재료나 하위 부품의 기대 수명에 따라 결정될 것이다. 시간 t2 이후, 고장률은 통계적으로 급격하게 증가하기 시작하는는데데, 이 단계를 마모 고장 (wear-out failure)이라고 한다. 발생 원인은 긴 동작 시간 또는 동작 온도, 습도, 기계적 진동 등에 따른 마모, 노화, 부식 등이 되겠다. 이에 대한 대책은 제품의 폐기, 또는 이러한 고장을 일으키는 하위 부품을 교체하는 예방 정비, 사후 보전 계획 등이 있을 수 있다. 복잡도가 낮고 가격이 비싸지 않은 제품의 경우 주로 폐기가 될 것이고, 자동차, 항공기와 같이 복잡도가 높고 가격이 매우 비싸며, 제품 레벨의 기대 수명보다 그 제품을 구성하는 특정 부품의 수명이 짧은 경우 주기적인 예방 보전을 통해 수명을 다한 부품이 고장을 일으키기 전에 교체하는 방법을 적용할 수 있다.
이제, 고장률에 대해 좀 더 자세히 정의해 보자. 먼저 EDH (Equivalent Device Hours)를 다음과 같이 정의한다.
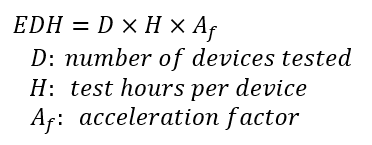
실험실 조건에서 EDH를 알아내기 위해서는, 한 개의 제품을 매우 오랜 시간동안 신뢰성 시험을 하는 것 보다, 많은 수의 제품을 상대적으로 짧은 시간동안 시험을 하는 것이 현실적인 방안이다. 고장률 (λ) 은 EDH를 이용하여 다음과 같이 정의된다.
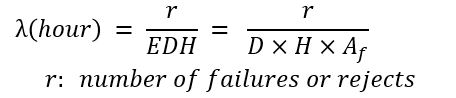
고장률 (λ) 에 대한 수식은 간단, 명료해 보이지만, 몇 가지 실무적인 문제가 있다. Number of failures or rejects, r의 경우, 어떤 제품이 필드에서 동작 중에 고장이 났다면, 그 제품이 어떠한 동작 조건이었는 지 알아야 한다. 제품의 공급사는 동일한 제품을 여러 고객에게 판매한다. 이 중 한 고객이 제품을 좀 더 높은 스트레스 환경에서 사용했다면, 이 고객사에서는 좀 더 많은 고장 개수를 가질 것이다. 또한 실제 고장난 제품 중 몇 개 정도가 회수 되는 지도 명확히 알기가 힘들다. 따라서 필드에서 고장이 회수되는 개수로 단순히 고장률을 계산하는 것은 합리적이지 않다. 따라서, 신뢰성 실험실 환경에서 통계적으로 정의된 r의 값 및 acceleration factor, Af를 가지고 고장률 (λ)을 계산하는 것이 일반적이다.
r, number of failures or rejects: 이 값은 카이제곱 분포를 이용한다. 가우시간 정규 분포를 따르는 확률변수 X의 n개의 샘플, x1, x2, x3, .. , xn의 합 또는 평균을 구하는 과정에서, 만약 이 샘플들을 단순히 더하는 것이 아니라 제곱을 하여 더하면 양수 값 만을 가지는 분포가 된다. 이것을 카이제곱 (chi-squared) 분포라고 한다. 카이제곱 분포에 대한 상세한 내용은 하기 링크를 참조해 보자.
https://ko.wikipedia.org/wiki/카이제곱_분포
http://blog.naver.com/PostView.nhn?blogId=mykepzzang&logNo=220852102307
기능안전에서 주로 카이제곱 분포를 r, number of failures or rejects를 위해 사용하는 방식은 다음과 같다.
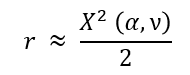
여기서 α 는 신뢰구간 (confidence level)을 의미하며, 카이제곱 확률분포 곡선의 적용구간을 의미한다. 고장률 예측에는 주로 α = 0.6 (= 60%)를 사용한다. 이 값의 최소, 최대치는 0.0 (0%) 및 1.0 (100%)이다.
ν 는 자유도 (degrees of freedom)를 의미하며, 카이제곱 확률분포 곡선의 형태와 관련이 있다. 자세한 의미는 상기의 link를 참조한다. 신뢰성 실험환경에서 ν는, 주어진 pass/fail criteria를 만족하지 못한 샘플이 나왔을 때, 그 횟수를 r, number of failures or rejects로 하고, 다음의 수식으로 계산한다.
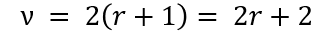
카이제곱 분포를 실무적으로 적용하기 위해 많이 사용하는 MS Excel함수가 CHIINV (probability, deg_freedom)이다. 이 함수를 이용한 고장률 예측을 하는 템플릿을 만들 수 있으며, 추후 별도의 주제로 다루어 보도록 한다.
이제 고장률 (λ)은 다음과 같이 정의할 수 있다.
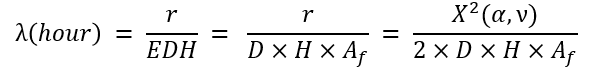
Af, acceleration factor: 이제 acceleration factor에 대해 알아보자. 물리학에서 아레니우스 방정식은 반응 속도의 온도 의존도를 나타내는 공식이다. 스웨덴의 물리학자인 스반테 아레니우스의 이름을 딴 것이다. 좀 더 자세한 내용은 아래 링크를 참조한다.
https://ko.wikipedia.org/wiki/아레니우스_방정식
Acceleration factor, Af는 아레니우스 방정식에서 유도된 것이다. 신뢰성 시험은 실제 제품 동작조건 보다 더 harsh한 조건이므로, 이 실험 조건 및 결과에 대응하는 acceleration factor를 예측하여 제품의 filed 고장률 계산에 사용한다. Acceleration factor, Af의 정의는 구체적으로는 각 시험 사양에 따라 다르게 정의할 수 있는데, HTOL (High Temperature Operating Life) 또는 Burn-in Test의 경우에는 다음과 같은 식이 사용된다.
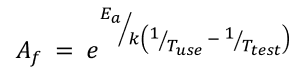
여기서, Ea는 activation energy라고 하며, [eV], electron volts라는 에너지 단위가 사용된다. 1 [eV]는 단위 전자가 1[V]의 전위차를 가진 공간을 거슬러 올라 갈 때 필요한 에너지이다. 줄 에너지와 환산은 다음과 같다. 1 [eV] = 1.60217646 x 10^-19 [J]. Activation energy에 대한 물리적인 의미는 어떠한 주어진 형태의 부품 또는 재료가 어떠한 형태의 failure mode를 유발하도록 하는 최소한의 에너지를 실험적으로 구한 것이라 할 수 있다. 이러한 failure mode는 구체적으로 oxidation defects, bulk silicon defects, mask defects, electro-migration or contamination defects 등이 될 수 있다. Diode type의 반도체 소자로 만들어진 부품의 경우, 통용되는 activation energy는 Ea = 0.7 [eV] 이다.
k는 볼츠만 상수 (Boltzmann’s Constant) 이며 8.617 x 10^-5 [eV/deg_K]의 값을 가진다. Tuse는 제품의 평균 사용온도이며, 55[degC] 또는 절대온도 328[degK]가 될 수 있다. Ttest는 HTOL 조건에서 시험온도이다. 수식에서는 절대온도 degK가 사용된다. 볼츠만 상수는 입자 수준에서의 에너지와 거시 수준에서 관측된 온도를 연관시켜주는 물리 상수이며, 기체 상수와 아보가드로 수의 비이다.
FIT (Failure in Time) : 우발적 고장률, random failure (λ) 를 기능안전표준에서 사용할 때 정의하는 용어이다. λ_FIT으로 표기하며, λ_hours와의 관계는 다음과 같다.
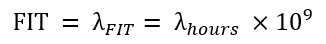
상기에서 검토한, acceleration factor, Af를 감안한 EDH (Equivalent Device Hours)가 10억 시간일 때 number of failures or rejects, r를 카이제곱 분포를 이용하여 구한 것이라고 정의할 수 있다.
MTTF (Mean Time to Failure): 이 값은 고장에 도달하기 까지 걸리는 평균 시간을 의미하며, 앞서 구한 고장율 (λ) 의 역수로 정의할 수 있다. 실무에서는 주로 MTTF_years를 사용하게 된다.

MTTF는 수리를 하기 힘들고, 고장 발생 시 폐기 해야 하는 제품에 주로 사용된다. 예를 들어 자동차용 센서의 경우, 보통 자동차의 기대 수명 동안 정상동작하도록 요구되고 있으며, 인공위성과 같은 복잡한 시스템이나, 그에 소요되는 부품의 경우에도 마찬가지로 수리가 불가한 조건이다.
MTBF (Mean Time between Failures): MTTF에 반하여, MTBF는 제품 고장과 고장사이에 소요되는 시간을 의미하며, 산업계에서는 고장과 고장 사이의 시간을 예측하고, 사전에 예방 정비를 통하여, 그 제품이 사용되는 좀 더 복잡한 상위 개념의 시스템이 지속적으로 성능을 발휘하도록 하는 데 사용된다. 예를 들면 비행기를 생각해 볼 수 있다. 비행기를 구성하는 각 부품은 각각의 MTBF가 있으며, 각 부품을 예방정비계획에 따라 사전에 교체를 하여, 그 부품의 우발고장으로 인한 사고를 미연에 방지하는 용도로 사용할 수 있다. MTTF와 별 차이가 없는 용어라 생각할 수 있으나, 사용되는 용도를 보았을 때 좀 더 보수적으로 다루어 져야 한다. MTBF의 실제 사용되는 정의에는 많은 variation이 있다. 좀 더 구체적으로 살펴보려면 하기 링크를 참조 한다.
https://en.wikipedia.org/wiki/Mean_time_between_failures
이제 FIT에 대한 정의는 살펴보았고, 이것을 실무에 어떻게 적용해야 하는 지에 대한 의문이 남는다. 센서나 전자 모듈을 생각해 보자. 그것은 소자, 재료, 수동전자부품 (R, L, C류), 트랜지스터나 다이오드 같은 개별 descrete류 부품, RAM이나 ROM같은 기능 단위별 IC, ADC와 DAC같은 아날로그-디지털 변환소자, MCU와 같은 CPU와 bus, 필수 peripheral 등으로 구성된 controller unit 등을 가지고 있을 것이다. Wire bonding이나 PCB등도 고려 대상이 될 수 있다. 하나의 제품을 구성하는 이러한 소재, 부품류의 FIT 값을 모두 알수 있어야 제품단위의 FIT값을 계산할 수 있을 것이다. 그러면 모든 부품에 대해 상기에서 살펴본 바와 같은 프로세스를 진행해야 하는가? 모든 것을 직접할 필요는 없고, 해당 부품사에 연락하여 FIT 값을 제출하라고 요청할 수 있다. 하지만, 실무적으로는 여러 가지 어려움이 따를 수 있는데, 예컨대, 해당 부품사가 그 값 자체를 제공할 수 없을 수도 있고, 일부 자체 개발한 부품이나 소재류, 제조 공정의 결과물일 경우 직접 그 값을 구해야 할 수도 있다. 또한 각 부품마다 FIT을 계산할 때 다른 기준을 가졌다면 (confidene level, 또는 평균 온도 등), 그것을 어떻게 통합하고 제품 레벨의 FIT을 구할 수 있을 것인가? 또한, 제공 받은 데이터의 신뢰도가 부품 공급사마다 다를 것을 우려하는 경우, 최종적으로 계산한 제품 레벨의 FIT는 어떻게 신뢰할 수 있는가?
이러한 문제를 해결하고, 좀 더 객관적으로 failure rate를 계산하기 위하여 기능안전프로세스에서는 failure rate handbook이라는 것을 사용한다. 주로 사용되는 것으로는 Siemens Norm, SN29500 / ICE TR 62380 / Mil Handbook, MIL-HDBK-271F 등이 있다. 이 중에 사용빈도가 가장 높은 Siemens Norm, SN29500을 살펴보면 일반적인 IC, descrete소자류, 수동 소자류, 릴레이, 스위치, 버튼류 등등에 대해 FIT값 및 그 값을 사용하기 위한 환산 방법을 제안하고 있다. 하지만, 여전히 개발자가 직접 만든 ASIC이나, 센서의 소재, 부품, 공정결과물은 직접 값을 도출해 내야 할 것이며, 이 경우는 앞서 설명한 내용이 그 프로세스가 될 것이다.