휘이스톤 브릿지 (Wheatstone bridge) 는 저항 반응형 소자에 의해 동작하는 센서를 설계하는 데 많이 사용된다. 실제 Application은 실리콘 재료의 압저항 효과를 이용한 압력센서, MR (Magneto-resistive), 저항 반응 형 습도 센서 등이 있다. 이러한 센서 브릿지의 기본 원리 및 Application에 대해서는 잘 알려져 있다.
그런데, 대부분의 설계 과정에서 휘이스톤 브릿지 자체의 입력 임피던스 및 출력 임피던스에 대해서는 별로 고민을 하지 않는 것 같다. 하지만, 그러한 센서 브릿지가 다음 단계의 회로 연결에서 항상 이상적인 High impedance 상태로 된다는 보장도 할 수 없고, EMC 성능 향상 등의 목적으로 센서 브릿지 출력 측에 Capacitor를 달아 Low pass filter 기능을 가지도록 하기도 한다. 이 경우, 센서 브릿지 자체의 입력 임피던스 및 출력 임피던스를 계산해야, 정확한 필터 정수 설계 등이 가능해 진다.
다음의 회로와 같이 1개의 Full 브릿지 회로가 있고, 양 측 출력에 Capacitor가 하나 씩 달려 있는 Sensing element 구성에 대해 알아보자. 보통 R-C로 구성된 Low pass filter의 경우 필터의 통과대역/저지대역을 정의하는 Cut-off frequency는, -3dB감쇄 기준으로 1/(2*pi*R*C) [Hz]이다. 이때에는 R과 C가 정해져 있으므로 바로 계산이 된다. 하지만, 아래 그림 처럼 센서 브릿지에 Capacitor가 달려 있는 경우는 어떻게 되는 것일까? 또한 R1, R2, R3, R4는 모두 센서 동작에 따라 저항 값이 변화하는 센서소자(Strain gage)이다. 이 것이 변화 하면 센서 브릿지의 입/출력 임피던스 값이나, 필터의 Cut-off frequency에는 어떠한 영향을 미치게 될까?
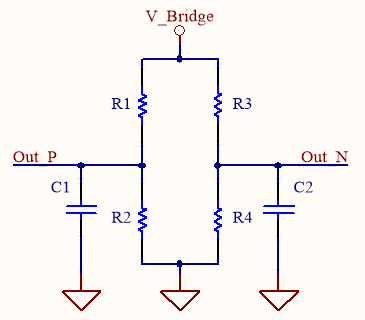
Output Impedance of Wheatstone Bridge
먼저 Capacitor를 제거하고, 센서 브릿지 회로만 보도록 한다. 대부분의 설계 예에서, 모든 저항의 공칭 값은 동일하게 하고, 압저항 효과에 의해 저항 값이 변화 될 때 R1, R4는 증가, R2, R4는 감소하는 방향으로 센서 엘리먼트 설계를 한다 (또는 그 반대 방향). 실제 센서의 특성은 설계 조건, 또는 제조 조건에 따른 편차가 존재하나, 센서 브릿지의 임피던스를 알아보는 과정에서는 그 편차가 실제 운용조건에서도 크게 영향을 주지 않으므로, 다음과 같이 이상적으로 정의해도 된다.
- R1 = R2 = R3 = R4 = R , when no strain is applied to the strain gage
- 압저항 효과에 의해 각 Strain gage에 생기는 저항 변화를 rp라고 하면,
- R1 = R + rp, R2 = R – rp, R3 = R – rp, R4 = R + rp 가 된다.
센서 브릿지 회로는 다음과 같이 되는데, 좌측 (A) 부터 (B), (C) 까지의 변화 과정을 정의해 보도록 한다.
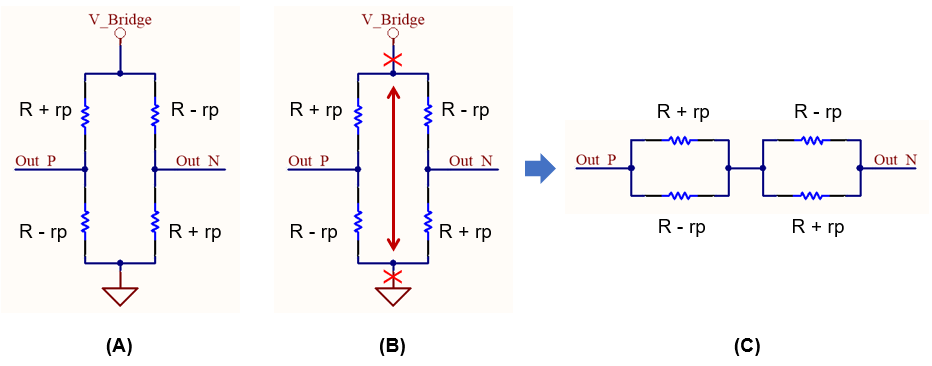
센서 브릿지 회로에서 입력 임피던스는, ASIC이 센서 브릿지를 drive 할 때 임피던스 값을 의미한다. 회로 (A)에서, Out_P, Out_N에 연결되는 다음 단의 회로는 High impedance를 가진 Amp 입력단이므로 입력 임피던스 고려사항에서 제외 될 수 있다. 좌측 Half bridge 및 우측 Half bridge 각각은 직렬 연결되어 있다. 좌측 Half bridge 값은 R + rp + R – rp = 2R이고, 이는 우측 Half bridge와 같다. 그리고 좌측 및 우측 Half bridge는 같은 값, 2R로 병렬 연결되므로, V_Bridge와 GND 양 측면에서 본 입력 임피던스는 R 이 된다. 이는 센서의 동작에 따른 Strain gage의 저항값 변화, rp의 크기 여부에 관련이 없다.
출력 임피던스의 경우에는 입력 임피던스와 같이 간단히 해결되지는 않는다. 출력 임피던스는 센서 브릿지에 전원이 공급되고 있고, 센서 브릿지가 작동하는 조건이 고려되어야 한다. 예를 들면, V_Bridge는 5V, GND는 0V가 될 것이다. 전원 공급장치는 내부 저항을 가지고 있으나, 이 값은 충분히 작아야 한다 (발열 및 효율성 문제). 이상적인 경우에는 0 [Ohm]으로 볼 수 있다. 그러면, 회로 (A)는 회로 (B)와 같이 V_Bridge와 GND로 연결되는 네트를 끊고, 센서 브릿지의 Top와 Bottom이 서로 연결된 상태 (빨간색 화살표) 로 생각할 수 있다. 이 회로를 보기 쉽게 정리하면 (C)와 같이 된다. 따라서, 이 회로도 (C)에서 Out_P와 Out_N 사이에서 측정할 수 있는 저항 값이 출력 임피던스로 정의된다.
R + rp와 R – rp의 직렬 연결은 단순히 2R이 되나, 회로도 (C)와 같이 병렬 연결된 경우는 다음과 같이 된다. rp 항이 존재하므로, 출력 임피던스는 Strain gage의 동작에 영향을 받는 것을 알 수 있다.
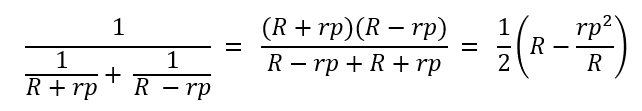
이러한 병렬 연결이 2개 직결로 연결되어 있으므로, Out_P와 Out_N 양측에서 측정되는 출력임피던스는 다음과 같이 된다.
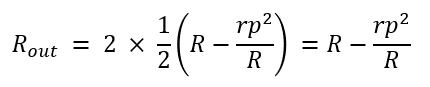
Low Pass Filter Design at Sensor Bridge
결과에서 보면, Strain gage 동작에 따라 변화하는 저항값 rp가 얼마나 되는 지 가늠하기 어렵다. 실제 이러한 압저항 효과를 이용한 MEMS 압력센서의 사양을 가지고 확인을 해 보도록 한다.
(Example) MEMS Pressure Sensor with Specification, as follow;
- Operating Pressure Range: 20 [Bar, abs]
- Span, Full Scale: 18 [mV/V, typ]
- Offset, Full Sale: +/-10 [mV/V]
- Bridge Resistance: 5.4 [KOhm]
- 기타 사양 항목 생략
V_Bridge가 5V 라고 하면, 20 [Bar]에서 센서 브릿지 출력이 18 x 5 = 90 [mV]가 나온다. 이 센서는 풀 브릿지 타입 이므로, 상기 그림 (A)의 Out_P는 2.5V에서 -0.045V 만큼 약간 작게 감소, Out_N은 2.5V에서 +0.045V 만큼 약간 크게 증가한다. 따라서, 그림 (A)의 우측 Half 브릿지에서, 다음 과정을 통해 rp값을 계산할 수 있다.
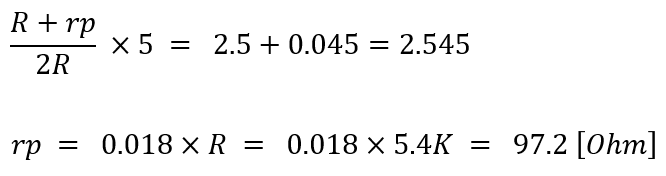
압력이 0 [Bar]에서 20 [Bar]로 변화 할 때, 각 strain gage의 저항 변화는, Bridge Resistance 5.4 [KOhm]에서 1.8 [%]변화된 97.2 [Ohm]이라는 것을 알 수 있다. 이 값을 이용하여 센서 브릿지의 출력 임피던스 변화를 계산 해 보면,
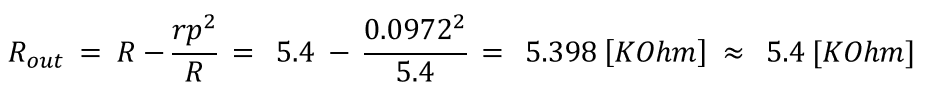
결과를 고찰해 보면, 출력 임피던스의 변화가 무시할 만한 정도라는 것을 알 수 있다. Analog LPF에 Capacitor를 1 [nF]을 사용했다면, 컷오프 주파수 수식 1/(2*pi*R*C) [Hz]에 의해, 0 [Bar] 일 때는 58.976 [KHz]가 되고, 20 [Bar] 일 때는 58.998 [KHz]가 된다. 이 편차도 무시할 만 한다. 따라서, 대부분의 설계에서 센서 브릿지의 출력임피던스에 Strain gage동작에 의한 영향을 생각할 필요 없이 센서 브릿지의 전체 저항 값인 5.4 [KOhm]을 사용해도 된다. 다만, 이 계산에서는 5.4 [KOhm]의 절반인 2.7 [KOhm]이 사용되었다. 그 이유는, 센서 브릿지는 통상 Single Power Supply에 의해 동작하고 (한 쪽이 Ground), 센서 브릿지의 좌, 우측에 각각 LPF가 있으며, 센서 브릿지로 부터 Analog front-end & 최종 ADC Conversion까지는 Virtual Ground (통상 공급 전압의 50%, 여기서는 2.5V)를 기준으로 동작한다. 따라서 센서 브릿지의 출력 임피던스는 5.4[KOhm]이 좌측 Half bridge 및 우측 Half bridge에 각각 절반 씩 할당되어 있다고 정의할 수 있다. 결과를 보면, 복잡한 과정이 필요 없이, 센서 브릿지의 입력 임피던스나 출력 임피던스는 같다고 가정할 수 있다. 하지만 차이점에 대해서 정확히 아는 것은 필요한 과정일 것이다.